3264 and all that
Resources
We are reading 3264 and all that by David Eisenbud and Joe Harris. If you’d like to be kept updated, please join the mailing list.
Schedule
We are meeting on Fridays from 5-6 PM.
| Date | Speaker | Reading |
|---|---|---|
| Week 1 (2/10) | John Cobb | 1.2 and 1.3.1-1.3.5 The Chow ring (16 pages) |
| Week 2 (2/17) | Kevin Dao | 1.3.6-1.4 Functoriality, transversality, canonical classes (14 pages) |
| Week 3 (2/24) | Alejo Salvatore | 2.1.1-2.1.7 Computing examples (11 pages) |
| Week 4 (3/3) | John Cobb | 2.1.9-2.3 Computing more examples (13 pages) |
| Week 5 (3/10) | John Cobb | 2.4-2.5 Curves on Surfaces (10 pages) |
| Week 6 (3/24) | John Cobb | 3.1-3.2 Intro to Grassmannians (17 pages) |
| Week 7 & 8 (4/7-4/13) | John Cobb | 3.3-3.4 \(\mathbb{G}(1,3)\) (13 pages) |
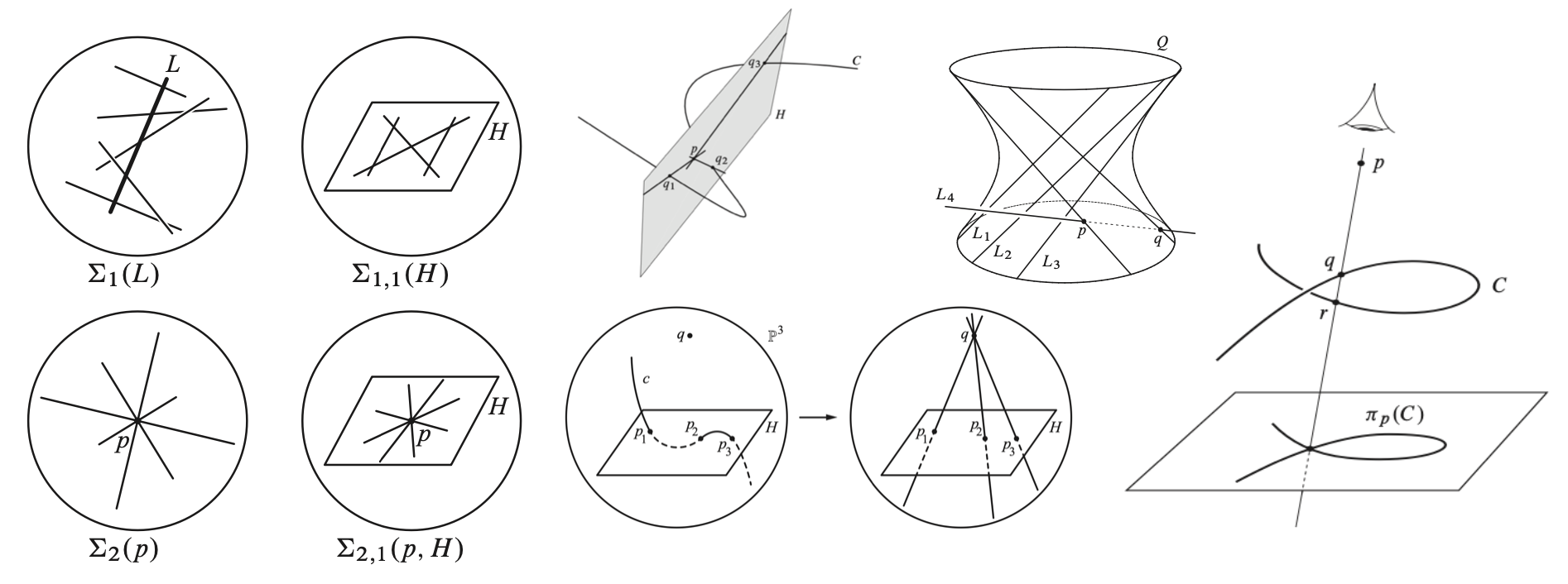
| Week 9 (4/21) | John Cobb | 3.5-3.6 Lines and surfaces in \(\mathbb{P}^3\) (18 pages) |
| Week 10 (4/28) | TBA | Ch. 4 Generalizing to all Grassmannians (34 pages) |
| Week 11 (5/5) | TBA | Ch. 5 Chern Classes (28 pages) or Fano and Hilbert Schemes (15 pages) |
Meeting Structure
While reading, write any questions you have and bring them. Each week the speaker will be giving a ~15 minute talk summarizing the reading that week (maybe bullet-point style), skipping proofs and focusing on how to use the theorems and objects. Note that being the speaker does not mean you are expected to know everything – You can have lots of questions too. After, we can all discuss questions we had on the reading.